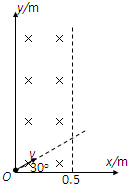
如图所示,以O为原点建立平面直角坐标系Oxy,沿y轴放置一平面荧光屏,在y>0,0<x<0.5m的区域有垂直于纸面向里的匀强磁场,磁场的磁感应强度大小B=0.5T.在原点O放一个开有小孔粒子源,粒子源能同时放出比荷为q/m=4.0×106kg/C的不同速率的正离子束,沿与x轴成30°角从小孔射入磁场,最后打在荧光屏上,使荧光屏发亮.入射正离子束的速率在0到最大值vm=2.0×106m/s的范围内,不计离子之间的相互作用,也不计离子的重力.
(1)求离子打到荧光屏上的范围.
(2)若在某时刻(设为t=0时刻)沿与x轴成30°角方向射入各种速率的正离子,求经过
×10-7s时这些离子所在位置构成的曲线方程.5π 3
(3)实际上,从O点射入的正离子束有一定的宽度,设正离子将在与x轴成30°~60°角内进入磁场.则某时刻(设为t=0时刻)在这一宽度内向各个方向射入各种速率的离子,求经过
×10-7s时这些离子可能出现的区域面积.5π 3
(1)由qvB=
得,r=mv2 r
,rm=mv qB
=1mmvm qB

离子在磁场中运动最大轨道半径:rm=1m
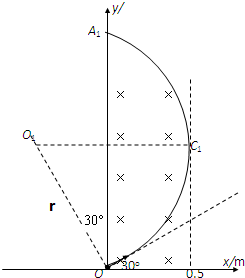
由几何关系知,最大速度的离子刚好沿磁场边缘打在荧光屏上,如左图所示.
所以OA1长度为:y=2rcos300=
m3
即离子打到荧光屏上的范围为:[0,
m]3
(2)离子在磁场中运动的周期为:T=
=π×10-6s2πm qB
由题,经过时间:t=
×10-7s,则5π 3
离子转过的圆心角为 φ=
t=2π T π 3
设
×10-7s这个时刻某离子的位置坐标为(x,y),则有5π 3
y=rcos30°
x=r-rsin30°
所以解得:y=
x就是所求的曲线方程.3
(3)由几何关系知,与x轴成60°方向入射的离子,经过时间:t=
×10-7s时离子转过的圆心角为φ=5π 3
t=2π T
刚好打在y轴上,将t=π 3
×10-7s时刻这些离子所在坐标连成曲线,方程就是:x=0即都打在y轴上,所以在t=0时刻与x轴成30°~60°内进入磁场的正离子在t=5π 3
×10-7s时刻全部出现在以O为圆心的扇形OA2C1范围内.如图 5π 3
则离子可能出现的区域面积:S=
=πrm2 12
m2≈0.26m2π 12
答:
(1)离子打到荧光屏上的范围为[0,
m].3
(2)经过
×10-7s时这些离子所在位置构成的曲线方程是y=5π 3
x.3
(3)经过
×10-7s时这些离子可能出现的区域面积为0.26m2.5π 3
