如图所示是一种简化磁约束示意图，可以将高能粒子约束起来．有一个环形匀强磁场区域的截面内半径R1，外半径R2，被约束的粒子带正电，比荷
=4.0×107C/kg，不计粒子重力和粒子间相互作用．（请在答卷中简要作出粒子运动轨迹图）q m
（1）若内半径R1=1m，外半径R2=3m，要使从中间区域沿任何方向，速率v=4×
107m/s的粒子射入磁场时都不能越出磁场的外边界，则磁场的磁感应强度B至少为多大？
（2）若内半径R1=
m，外半径R2=3m，磁感应强度B=0.5T，带电粒子从中间区域沿半径方向射入磁场，则粒子不能穿越磁场外边界的最大速率vm是多少？3
（3）若带电粒子以（2）问中最大速率vm从圆心O出发沿圆环半径方向射入磁场，请在图中画出其运动轨迹，并求出粒子从出发到第二次回到出发点所用的时间（结果可用分数表示或保留二位有效数字）．
（1）粒子在匀强磁场中做匀速圆周运动，磁感应强度越，粒子轨道半径越大，
求出最大轨道半径，然后求出对应的最小磁感应强度，粒子轨道半径最大时，运动轨迹如图所示：
由图示可知，r2+R12=（R2-r）2，
粒子在磁场中做匀速圆周运动，
由牛顿第二定律得：qvB=m
，v2 r
解得：B=0.75T，则磁感应强度至少为0.75T；
（2）粒子沿半径方向射出恰好不射出磁场时的运动轨迹如图所示：
根据图示，由数学知识可知：r2+R12=（R2-r）2，
将R1=
m，R2=3m代入解得：r=1m，3
粒子在磁场中做匀速圆周运动，
由牛顿第二定律得：qvB=m
，v2 r
已知：B=0.5T，
解得：v=2×107m/s，
则粒子的最大速率为2×107m/s．
（3）带电粒子必须三次经过磁场，才能回到出发点，轨迹如图所示：
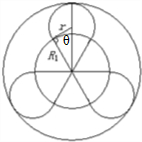根据图示由数学知识可知，tanθ=
=R1 r
，则θ=60°3
则粒子在磁场中运动一次转过的圆心角φ=360-2×60=240°，
粒子在磁场中的运动时间：
t1=3
T=3×φ 360°
×240° 360°
=2π×10-7s≈6.28×10-7s，2πm qB
粒子在磁场外的运动时间：
t2=3
=3×2R1 v
≈5.20×10-7s，2× 3 2×107
粒子从出发到第二次回到出发点所用的时间t=t1+t2≈1.1×10-6s，
答：（1）磁场的磁感应强度B至少为0.75T；
（2）粒子不能穿越磁场外边界的最大速率vm是2×107m/s；
（3）粒子从出发到第二次回到出发点所用的时间为1.1×10-6s．
