在平面直角坐标系的第一象限内存在一有界匀强磁场，该磁场的磁感

问题问答题

在平面直角坐标系的第一象限内存在一有界匀强磁场，该磁场的磁感应强度大小为B=0.1T，方向垂直于xOy平面向里，在坐标原点O处有一正离子放射源，放射出的正离子的比荷都为

=1×10⁶C/kg，且速度方向与磁场方向垂直．若各离子间的相互作用和离子的重力都可以忽略不计．

（1）如图甲所示，若第一象限存在直角三角形AOC的有界磁场，∠OAC=30°，AO边的长度l=0.3m，正离子从O点沿x轴正方向以某一速度射入，要使离子恰好能从AC边射出，求离子的速度大小及离子在磁场中运动的时间．

（2）如图乙所示，若第一象限存在一未知位置的有界匀强磁场，正离子放射源放射出不同速度的离子，所有正离子入射磁场的方向均沿x轴正方向，且最大速度v_m=4.0×10⁴m/s，为保证所有离子离开磁场的时候，速度方向都沿y轴正方向，试求磁场的最小面积，并在图乙中画出它的形状．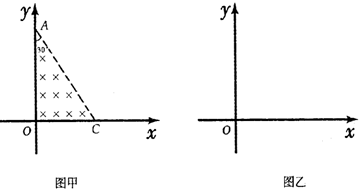

答案

（1）正离子在磁场内做匀速圆周运动，离子刚好从AC边上的D点射出时，如图甲所示，离子轨迹圆的圆心为O′，轨道半径为r，由几何知识得：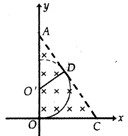

r+2r=l

故r=

=0.1m

粒子在磁场中运动，洛伦兹力提供向心力

qvB=m

联立以上各式的：v=

qBr

=1.0×10⁴m/s

若正离子恰好从AC边射出，由几何知识可知，圆心角∠DO′O=120°

又因T=

2πm

所以正离子在磁场中运动的时间t=

360°

T=2.1×10^-5s

（2）所有离子进入磁场后均做逆时针方向的匀速圆周运动，且入射方向沿x轴正方向，离开时沿y轴正方向，速度偏转角为

，并且所有离子的轨迹圆的圆心都在y轴正半轴上，

所以满足题意的最小磁场区域为图乙所示，

根据牛顿第二定律有：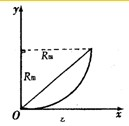

qv_mB=m

vm2

得：R_m=

mvm

=0.4m

所以磁场区域最小面积为：

πR_m²-

R_m²=0.04（π-2）=0.0456m²

答：（1）离子的速度大小为1.0×10⁴m/s，离子在磁场中运动的时间为2.1×10^-5s．

（2）磁场的最小面积为0.0456m²．