问题
问答题
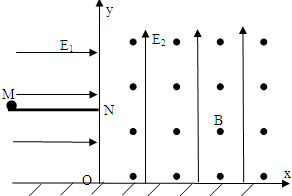
如图所示，坐标系xOy在竖直平面内，光滑且绝缘的水平轨道MN的长度为L，N点到O点的竖直距NO=
L．有一质量为m、电荷量为+q的带电小球（可看成质点）放在M点．已知在第一象限分布着互相垂直的匀强电场和匀强磁场，电场方向竖直向上，场强E2=3 2
；磁场方向水平（图中垂直纸面向外），磁感应强度大小为B；在第二象限分布着沿x轴正向的水平匀强电场，场强E1=mg q
．求B2qL 6m
（1）小球到达N点的速度大小
（2）小球到达x轴上的坐标
（3）小球从M点由静止释放至落到x轴上所需的时间（设运动过程中小球所带的电荷量不变）．
答案
（1）设带电小球运动到N点时速度为vN，由动能定理：
E1qL=
mvN21 2
解得：vN=3 3 BLq m
（2）当小球进入第一象限后，qE2=mg
所受电场力与重力平衡，所以带电小球将做匀速圆周运动：BqvN=mvN2 R
则小球做匀速圆周运动的半径R=
=mvN qB
L3 3
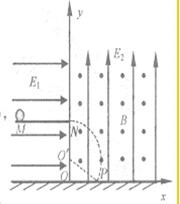
设圆周运动的圆心在图中的O′点，小球落点为P，O′O=NO-R=
L3 6
∠OO′P=arccos
=arccosOO′ R
=60°1 2
则带电粒子转过的圆心角为120°
到达x轴的位置到O点的距离为
R=3 2
L1 2
（3）设小球从M点运动到N点设用时为t1，则L=
a1t121 2
qE1=ma1
联立解得：t1=
，2
m3 qB
带电小球从N点运动到P点所用时间t2=
T=1 3
×2πm qB
=1 3 2πm 3qB
小球从M点出发到x轴的过程中所用时间t=t1+t2=
+2
m3 qB
．2πm 3qB
答：（1）小球到达N点的速度大小
．
BLq3 3m
（2）小球到达x轴上的坐标（
L，0）．1 2
（3）小球从M点由静止释放至落到x轴上所需的时间（设运动过程中小球所带的电荷量不变）
+2
m3 qB
．2πm 3qB
