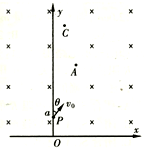
在如图所示的xoy坐标系中,仅在x轴上方有垂直于xoy平面向里、范围足够大的匀强磁场Ⅰ.质量为m,电荷量为q的负粒子在xoy平面内运动,某时刻经过y轴上y=a的P点,速度方向与y轴正方向夹角为θ=30°,经过时间t0粒子第一次经过x轴,速度方向与粒子在P点速度方向相反,不计重力.
(1)求粒子运动的速率v0和磁场Ⅰ的磁感应强度B1;
(2)若粒子经过P点时,在x轴上方再叠加一个方向垂直于xoy平面的匀强磁场Ⅱ,使粒子能在磁场中做完整的圆周运动,求匀强磁场Ⅱ的磁感应强度B2的大小和方向;
(3)若粒子经过P点时,加一方向在xoy平面内的匀强电场,粒子在复合场中运动时经过了A(2x0,yA)、C(x0,yC)两点,如图所示,粒子在A点的动能是P点动能的
,在C点的动能是P点动能的1 3
,求电场强度E的大小和方向.2 3
(1)粒子在磁场中运动半周,v0t0=πr,
圆周运动的半径r=
sinθ=a,a 2
解得:v0=πa t0
又t0=
T=1 2
,2πm qB1
解得:B1=πm qt0
(2)有两种情况: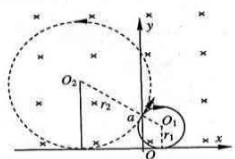
①B2与B1同向,粒子顺时针转动,若最大半径为r1,对应的(B1+B2)最小,
这时qv0(B1+B2)=mv 20 r1
r1+r1sin30°=a,
所以r1=2a 3
解得:B2=πm 2qt0
所以当B2方向垂直xoy平面向里时,应满足B2≥
(B2>πm 2qt0
亦可)πm 2qt0
②B2与B1反向,粒子逆时针转动的半径最大(设为r2)时,对应的(B2-B1)最小,
这时qv0(B2-B1)=mv 20 r2 
r2-r2sin30°=a,
解得:B22=3πm 2qt0
所以B2方向垂直xoy平面向外时,应满足B2≥
(B2>3πm 2qt0
亦可)3πm 2qt0
(3)粒子从P点到A点,-qUPA=
EkA-EkP1 3
粒子从P点到A点,-qUPC=
EkP-EkP2 3
解得:UPA=
=2UPCπ2ma2 3q t 20
即φP-φA=2(φP-φC),
所以:φC=φA+φP 2
所以C点电势与PA连线中点D等电势,
故电场方向沿+x方向,场强大小为:E=
=UPA 2x0
;π2ma2 6qx0 t 20
答:(1)粒子运动的速率v0为
磁场Ⅰ的磁感应强度B1为πa t0
;πm qt0
(2)若B2与B1同向,匀强磁场Ⅱ的磁感应强度B2的大小B2≥
;若B2与B1反向,匀强磁场Ⅱ的磁感应强度B2的大小B2>πm 2qt0
;πm 2qt0
(3)电场强度E的大小为
,方向沿+x方向.π2ma2 6qx0t02
