问题
问答题
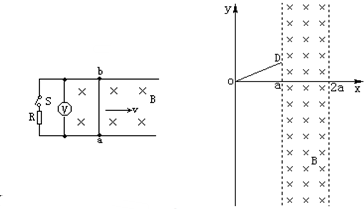
如图所示,坐标系xoy平面内的坐标原点O处有一粒子源,在某时刻发射大量质量为m、电荷量为q的带负电的粒子,它们的速度大小相同,速度方向均在xoy平面内.在直线x=a与x=2a之间存在垂直xoy平面向里的磁感应强度为B的匀强磁场,已知从坐标点D(a,
a)入射到磁场中的粒子垂直磁场边界射出,不计粒子的重力.求:3 3
(1)从D点入射的粒子在磁场中运动的时间;
(2)粒子的速率;
(3)在磁场中运动时间最长的粒子的运动时间.
答案
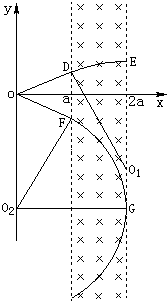
(1)作图,粒子从D点射入时,其轨迹的圆心在O1处,从E点垂直磁场右边界射出,
tan∠DOX=
a3 3 a
可得:∠DOX=30°,则∠DO1E=30°
从D点入射的粒子在磁场中运动的时间 t=
•30° 360°
=2πm Bq πm 6Bq
(2)由三角形知识可得:R=
=2aa sin300
由牛顿第二定律可得:qvB=mv2 R
可解得:v=2aqB m
(3)因粒子速率恒定,粒子在磁场中运动的轨迹越长时,时间越长,即当运动轨迹与右边界相切后从磁场的左边界射出时,运动轨迹最长,时间最长.由几何关系可知,
∠FO2G=60°
则圆弧对应的圆心角为120°,则最长时间 tm=
•1200 3600
=2πm Bq 2πm 3Bq
答:(1)从D点入射的粒子在磁场中运动的时间为
;(2)粒子的速率为πm 6Bq
;(3)在磁场中运动时间最长的粒子的运动时间为2aqB m
.2πm 3Bq