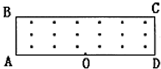
如图所示,在矩形区域内有垂直于纸平面向外的匀强磁场,磁感应强度大小为B=5.0×10-2T,矩形区域长为
m,宽为0.2m,在AD边中点O处有一放射源,某时刻,放射源沿纸面向磁场中各方向均匀地辐射出速率均为v=2×l06m/S的某种带正电粒子,带电粒子质量m=1.6×10-27kg.电荷量为q=+3.2×l0-19C(不计粒子重力),求:2 3 5
(1)带电粒子在磁场中做圆周运动的半径为多大?
(2)从BC边界射出的粒子中,在磁场中运动的最短时间为多少?
(3)若放射源向磁场内共辐射出了N个粒子,求从CD边界射出的粒子有多少个?
(1)洛伦兹力提供向心力:qvB=mv2 R
得:R=
=0.2mmv qB
(2)因为所有粒子的轨迹半径相同,所以弦最短的圆弧所对应的圆心角最小,运动时间最短.
作EO⊥AD,EO弦最短,
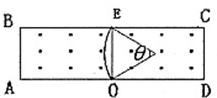
因为
=0.2m,且R=0.2m. EO
所以对应的圆心角为θ=π 3
又qvB=mR(
)22π T
得:T=2πm qB
则最短时间为:t=
=θm qB
=πm 3qB
×10-7sπ 3
(3)判断从O点哪些方向射入磁场的粒子将会从CD边射出,如图为两个边界,
当速度方向满足一定条件时,粒子将从D点射出磁场,
=. OD
m,且R=0.2m3 5
由三角函数知识可知∠OO2D=2π 3
此时射入磁场的粒子速度方向与OD夹角为
,π 3
当轨迹圆与BC边相切时,因为R=0.2m,
=0.2m,可知圆心O1在AD边上,. CD
因为
<. OO1 . OD
所以带电粒子不可能通过C点,
与BC相切的即为从CD边射出磁场的最上边缘的粒子,
该粒子进入磁场的速度方向垂直AD向上,与OD之间的夹角为
,π 2
所以从CD边射出的粒子,射入磁场时速度方向应与OD边夹角在
到π 3
之间△θ=π 2
的范围内,π 6
因为放射源向磁场内各方向均匀地辐射粒子,
所以能从CD边射出的粒子数目为:
n=
N△θ π
即:n=N 6
答:(1)带电粒子在磁场中做圆周运动的半径为0.2m;
(2)从BC边界射出的粒子中,在磁场中运动的最短时间为
×10-7s;π 3
(3)若放射源向磁场内共辐射出了N个粒子,从CD边界射出的粒子有
个.N 6
