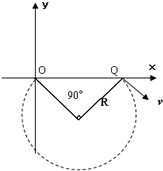
如图所示,x轴上方有一匀强电场,方向与y轴平行,x轴下方有一匀强磁场,方向垂直纸面向里,一质量为m、电量为-q(q>0)的粒子以速度v0从y轴上的P点平行x轴方向射入电场后,从x轴上的O点进入磁场,并从坐标原点O离开磁场,已知OP=L,OQ=2L,不计重力和一切阻力,求:
(1)粒子到达Q点时的速度大小和方向;
(2)粒子在磁场中运动的轨道半径;
(3)粒子在磁场中的运动时间.

(1)设粒子在电场中运动时间为t1,到达Q时竖直分速度为vy,速度大小为v,方向与x轴夹角为θ,由运动学公式得:
水平方向有:2L=v0t1
竖直方向有:L=
t0vy 2
联立解得:vy=v0,
则 v=
=v02+vy2
v0 2
tanθ=
=1,得θ=45° vy v0
(2)粒子在磁场中的轨迹如图所示,由几何关系可得粒子在磁场中的轨道半径:R=2 2
=. OQ
•2L=2 2
L2
(3)由图知,粒子在磁场中的运动时轨迹对应的圆心角为270°,则在磁场中运动的时间:
t2=
=270° 360°
T3 4
由圆周运动知识得:T=
=2πR v
v0=2π
L2 2 2πL v0
故得 t2=
T=3 4
×3 4
=2πL v0 3πL 2v0
答:(1)粒子到达Q点时的速度大小为
v0,方向与x轴成45°斜向下;2
(2)粒子在磁场中运动的轨道半径为
L;2
(3)粒子在磁场中的运动时间
.3πL 2v0