问题
填空题
已知平行四边形ABCD的两条对角线相交于点O，以
|
答案
∵△ABD中，
=AB
且a
=AD
，b
∴向量
=DB
-AB
=AD
-a b
∵四边形ABCD是平行四边形，
∴对角线交点O是BD的中点，
可得
=OB 1 2
=DB
（1 2
-a
）b
故答案为：
（1 2
-a
）b
搜题请搜索小程序“爱下问搜题”
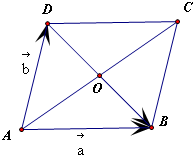
已知平行四边形ABCD的两条对角线相交于点O，以
|
∵△ABD中，
=AB
且a
=AD
，b
∴向量
=DB
-AB
=AD
-a b
∵四边形ABCD是平行四边形，
∴对角线交点O是BD的中点，
可得
=OB 1 2
=DB
（1 2
-a
）b
故答案为：
（1 2
-a
）b