问题
问答题
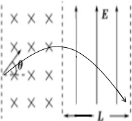
如图,某一初速度为v0的带电粒子进入一垂直于纸面向里、磁感应强度大小为B的有界匀强磁场,粒子垂直进入磁场时的速度与水平方向成θ=45°角,接着垂直进入一水平宽度为L、方向竖直向上的匀强电场(E大小未知),粒子穿出电场时速度大小变为原来的
| 2 |
(1)分析判断粒子的电性;
(2)求磁场的水平宽度d;
(3)求该匀强电场的电场强度E的大小.
答案
(1)粒子穿过磁场后进入电场,因此粒子在磁场中向下偏转,由左手定则可知,粒子带负电;
(2)设粒子的轨道半径为R,粒子在磁场中做匀速圆周运动,
由牛顿第二定律得:qv0B=m
| ||
| R |
由几何关系可得:d=Rsinθ,
解得:d=
| ||
| 2qB |
(3)粒子在电场中做类平抛运动,
粒子离开电场时的速度v=
| 2 |
v=
|
粒子在你电场中做类平抛运动,
L=v0t,y=
| vy |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由动能定理得:qE•
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:E=
m
| ||
| qL |
答:(1)粒子带负电;(2)磁场的水平宽度为
| ||
| 2qB |
m
| ||
| qL |