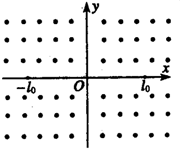
如图,在某装置中有一匀强磁场,磁感应强度为B,方向垂直于Oxy所在的纸面向外.某时刻在x=l0、y=0处,一质子沿y轴的负方向进入磁场;同一时刻,在x=-l0、y=0处,一个α粒子进入磁场,速度方向与磁场垂直.不考虑质子与α粒子的相互作用.质子的质量为m,电荷量为e.α粒子的质量是质子质量4倍,电荷量是质子电荷量的2倍.
(1)质子从x=l0处出发恰好经过坐标原点O,它的速度为多大?
(2)质子从x=l0处到达坐标原点O处的时间为多少?
(3)如果α粒子与质子经最短时间在坐标原点相遇,α粒子的速度应为何值?方向如何?
(1)质子从x=l0处出发恰好经过坐标原点O,知质子的轨道半径r1=
,l0 2 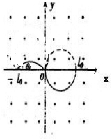
根据evB=mv2 r
解得质子的速度v=
=eBr1 m
;eBl0 2m
(2)质子在磁场中运动的周期T=
,2πm eB
则质子到达坐标原点O处的时间t=
=T 2
.πm eB
(3)α粒子的周期T′=
=2π•4m 2eB
,周期是质子周期的2倍,4πm eB
如果α粒子与质子经最短时间在坐标原点相遇,可知α粒子运动的时间为四分之一个周期.
即圆弧对应的圆心角为90度,根据几何关系知,α粒子的速度方向与x轴正方向成45°,
根据几何关系知,α粒子的轨道半径r2=
l0,2 2
根据半径公式r2=
,4mv′ 2eB
解得v′=
.
eBl02 4m
答:(1)质子从x=l0处出发恰好经过坐标原点O,它的速度为
;eBl0 2m
(2)质子从x=l0处到达坐标原点O处的时间为
;πm eB
(3)如果α粒子与质子经最短时间在坐标原点相遇,α粒子的速度应为
,方向与x轴的正方向成45°角.
eBl02 4m
