如图所示,一带电粒子从Y轴上的a点以平行于X轴的方向射入第一象限区域,射入的速度为v0.带电粒子的质量为m,带负电,电荷量为q.为了使带电粒子通过X轴上的b点,可在第一象限的某区域加一个沿Y轴正方向的匀强电场,电场强度为E,电场区域沿Y轴方向无限长,沿X方向的宽度为s.已知Oa=L,Ob=2s,不计带电粒子的重力.
(1)若b点在电场内,要使粒子过b点,求该电场的左边界与b点的距离.
(2)若b点在电场外,在第一象限紧挨电场右侧加一个垂直于XOY平面的磁感应强度为B的匀强磁场,该磁场足够大,使得粒子也能过b点且速度方向沿X轴正方向,求该电场的左边界与b点的距离.
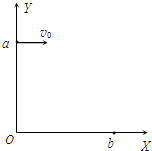
(1)带电粒子进入电场后沿X方向做匀速直线运动,沿Y方向做匀加速直线运动;
根据牛顿第二定律得,带电粒子在电场中运动的加速度大小为:
a=qE m
带电粒子进入电场后在X方向的位移为l,在Y方向的位移为L,如由图所示:根据运动学规律,有
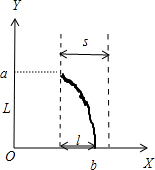
l=v0t
L=1 2
t2qE m
消去t,解得:
l=v02mL qE
即该电场的左边界与b点的距离为v0
;2mL qE
(2)分析可知,磁场方向应垂直XOY平面向外,粒子的运动轨迹如图所示.
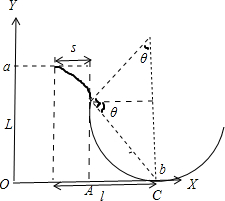
设粒子在磁场中的速率为v,运动半径为R,则
由Bqv=mv2 R
得R=mv qB
由几何关系可知:
AC=Rsinθ
所以l=s+AC=s+
sinθmv qB
其中:sinθ=
=at v qEs mv0v
所以:l=s+
•mv qB
=s+qEs mv0v
;Es Bv0
答:(1)电场的左边界与b点的距离v0
;2mL qE
(2)电场的左边界与b点的距离s+
.Es Bv0
