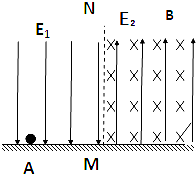
如图所示,虚线MN左侧的整个空间存在一方向竖直向下的匀强电场E1,虚线右侧的整个空间存在方向竖直向上的匀强电场E2和方向垂直纸面向内的匀强磁场B.一绝缘带电小球从距MN左侧的A点以一定的初速度向右运动,进入虚线右侧后在竖直面内做匀速圆周运动,向左穿过MN后恰好落回A点.已知A点到MN的距离为L;小球的质量为m、带电量为q,小球的初速度为v0,小球与水平面的动摩擦因数μ=v02/4gL;E1=mg/2q.
(1)求右侧电场E2的场强大小.
(2)求磁场B的磁感应强度大小.
(1)小球在MN右侧能做匀速圆周运动,则有
qE2=mg
解得,E2=
.mg q
(2)小球从A到M的过程中,设到M时速度为v.
由动能定理得:-μNL=
mv2-1 2
mv02;1 2
竖直方向平衡,有:N-qE1-mg=0
在右侧电磁场中粒子作匀速圆周运动:qvB=mv2 r
重新回到MN左侧运动作类平抛运动,则有:
L=vt
2r=
at21 2
根据牛顿第二定律得:mg+qE1=ma
由题μ=
;E1=v 20 4gL
.mg 2q
联立以上各式解得:B=m v 20 3gqL2
答:(1)右侧电场E2的场强大小是
.mg q
(2)磁场B的磁感应强度大小是:B=
.m v 20 3gqL2
