问题
问答题
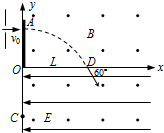
如图所示,在y轴右上方有一匀强磁场,磁感应强度为B,方向垂直纸面向外.在x轴的下方有一匀强电场,场强为E,方向平行x轴向左.有一铅板放置在y轴处且与纸面垂直.现有一质量为m、带电量为q的粒子由静止经过加速电压为U的电场加速,然后以垂直与铅板的方向从A处穿过铅板,而后从x轴的D处以与x轴正方向夹角为60°的方向进入电场和磁场重叠的区域,最后到达y轴上的C点.已知OD长为L,不计重力.求:
(1)粒子经过铅板时损失的动能;
(2)粒子到达C点时速度的大小.
答案
(1)根据洛伦兹力提供向心力得:qvB=mv2 r
由动能定理可知此带电粒子穿过铅板前的动能为:Ek0=qU
又由几何知识可得:
=sin60°L r
即:r=2L 3
所以:v=
=qBr m
,2qBL
m3
带电粒子穿过铅板后的动能:Ek=
mv2=1 2
,2q2B2L2 3m
因此粒子穿过铅板后动能的损失为:△Ek=Ek0-Ek=qU-2q2B2L2 3m
(2)从D到C只有电场力对粒子做功:
qEl=
m1 2
-v 2c
mv21 2
解得:vc=
+4q2B2L2 3m 2qEL m
答:(1)粒子经过铅板时损失的动能为△Ek=qU-
;2q2B2L2 3m
(2)粒子到达C点时的速度大小为 vc=
.
+2EqL m 4B2L2q2 3m2
