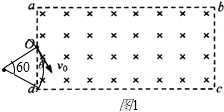
一足够长的矩形区域abcd内有磁感应强度为B,方向垂直纸面向里的匀强磁场,矩形区域的左边界ad宽为L,现从ad中点O垂直于磁场射入一带电粒子,速度大小为v0,方向与ad边夹角为θ=30°,如图所示.已知粒子的电荷量为q,质量为m(重力忽略不计).
(1)若粒子带负电,且恰好能从d点射出磁场,求v0的大小;
(2)若粒子带正电,使粒子能从ab边射出磁场,求v0的取值范围,以及此范围内粒子在磁场中运动时间t的范围.
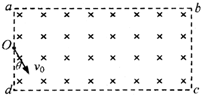
(1)若粒子带负电,且恰好能从d点射出磁场,它运动的轨迹如图1,
则运动的半径:R=
,L 2
运动的过程洛伦兹力提供向心力,得:qv0B=m v 20 R
整理得:ν0=BqL 2m
(2)若粒子带正电,粒子运动的轨迹如右图所示,当粒子的速度大于与R1相对应的速度v1时,粒子将从dc边射出.
由几何关系可得:R1=L①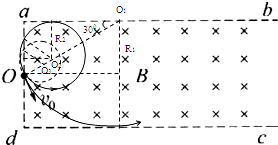
由洛仑兹力和向心力公式可得:qv1B=
②m v 21 R1
当粒子的速度小于与R2相对应的速度v2时,粒子将从ad边射出.
由几何关系可得:
L-R2=1 2
R2 ③1 2
由③式解得:R2=
L ④1 3
由洛仑兹力和向心力公式可得:qv2B=
⑤m v 22 R2
将①④式分别代入②⑤式可解得:v1=
;v2=qBL m
⑥qBL 3m
所以v0的取值范围是
≤v0≤qBL 3m
⑦qBL m
从图中可以看出,当轨迹的半径对应R1时从ab边上射出使用的时间最短,此时对应的圆心角为:
θ=180°-30°=150°
由公式可得:T=
=2πR v
⑧2πm qB
根据周期与运动时间的关系得:
=θ 360° t1 T
整理得:t1=
⑨5πm 6qB
粒子在磁场中运动的时间最长,其做圆周运动的圆心角必然最大,在答图中,当粒子的速度小于v2时,粒子从ad边的不同位置射出时,其半径虽不同,但圆心角的夹角都是300°=
×2π,所以粒子在磁场中的运动时间也是5 6
,此即粒子在磁场中运动的最长时间.5T 6
所以粒子运动的最长时间为:t2=
=5T 6
⑩5πm 3qB
与粒子在磁场中运行时间相对应的t的大小范围是
<t≤5πm 6Bq
:5πm 3Bq
答:(1)ν0=
(2)v0的取值范围BqL 2m
≤ν0≤BqL 3m
,粒子在磁场中运动时间t的范围BqL m
<t≤5πm 6Bq
.5πm 3Bq
