问题
解答题
已知向量a=(sinθ,cosθ-2sinθ),b=(1,2)。
(1)若a∥b,求tanθ的值;
(2)若|a|=|b|,0<θ<π,求θ的值。
答案
解:(1)因为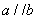 ,
,
所以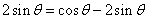 ,
,
于是4sinθ=cosθ,
故tanθ=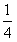 。
。
(2)由|a|=|b|
∴sin2θ+(cosθ-2sinθ)2=5
即1-2sin2θ+4sin2θ=5
化简得sin2θ+cos2θ=-1
故有sin(2θ+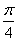 )=-
)=-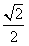
又∵θ∈(0,π)
∴2θ+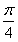 ∈(
∈(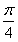 ,
,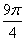 )
)
∴2θ+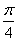 =
=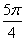 或2θ=
或2θ=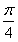 =
=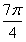
∴θ=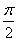 或θ=
或θ=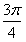 。
。
