如图所示,在xOy平面的第一象限有一匀强磁场,电场的方向平行于y轴向下:在x轴和第四象限的射线OC之间有一匀强磁场,磁感应强度的大小为B,方向垂直于纸面向外,有一质量为m,带有电荷量+q的粒子由电场左侧平行于x轴射入电场,粒子到x轴上A点时,速度方向与x轴的夹角为φ,A点与原点O的距离为d,接着粒子进入磁场,并垂直于OC边离开磁场,不计重力影响,若OC与x轴的夹角也为φ,求:
(1)粒子在磁场中运动速度的大小;
(2)匀强电场的场强大小;
(3)求带电粒子再次回到y轴所用的时间.
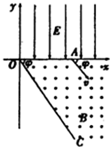
(1)设圆周运动的半径为R,由几何关系得:R=dsin φ
由洛仑兹力公式和牛顿第二定律得qvB=mv2 R
解得:v=qBdsinφ m
(2)质点在电场中的运动为类平抛运动.设质点射入电场的速度为v0,在电场中的加速度为a,运动时间为t,则有:v0=vcosφ
vsinφ=at
d=v0t
解得:a=v2sinφcosφ d
设电场强度的大小为E,由牛顿第二定律得
qE=ma
解得:E=
sin3φcosφqB2d m
(3)质点在电场中的运动为类平抛运动.设时间为t1,则:t1=d vcosφ
在匀强磁场中做匀速圆周运动,设时间为:t2则:
t2=
=T 4 πm 2qB

离开磁场后做匀速直线运动,设经过时间t3再次回到y轴.则:
t3=d(cosφ+sinφ) vtanφ
所以质点再次回到y轴的时间是:t=t1+t2+t3=
+d vcosφ
+πm 2qB d(cosφ+sinφ) vtanφ
答:(1)粒子在磁场中的速度为
;(2)匀强电场的大小为qBdsinφ m
sin3φcosφ;(3)带电粒子再次回到y轴所用的时间是qB2d m
+d vcosφ
+πm 2qB d(cosφ+sinφ) vtanφ
