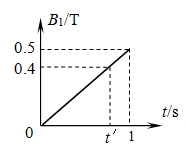
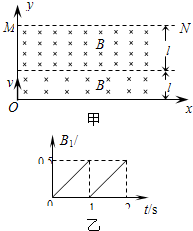
如图甲所示,x方向足够长的两个条形区域,其y方向的宽度分别为l1=0.1m和l2=0.2m,两区域分别分布着磁感应强度为B1和B2的磁场,磁场方与xy平面垂直向里,磁感应强度B2=0.1T,B1随时间变化的图象如图乙所示.现有大量粒子从坐标原点O以恒定速度v=2×106m/s不断沿y轴正方向射入磁场,已知带电粒子的电量q=-2×10-8C,质量m=4×10-16kg,不考虑磁场变化产生的电场及带电粒子的重力.求:
(1)在图乙中0~1s内,哪段时间从O发射的粒子能进入磁感应强度B2的磁场?
(2)带电粒子打在磁场上边界MN上的x坐标范围是多少?
(3)在MN以下整个磁场区域内,单个带电粒子运动的最长时间和最短时间分别是多少?
(1)粒子在B1磁场中运动时间极短,可视这极短时间内的磁场为恒定的匀强磁场,带电粒子在该磁场中做匀速圆周运动,根据牛顿第二定律,有
qvB1=m
,当r=l1时,B1=v2 r
,代入数据得mv ql1
B1=0.4T.
由右图可知,当B1=0.4T时,
t=t′=0.8s
因此,0~0.8s时间内B1的值小于0.4T,粒子运动半径大于l1,这段时间从O发射的粒子将进入磁感应强度B2的区域.
(2)设粒子在B2磁场中运动的半径为r2,当B1=0时,粒子打在MN上的A1点为最左边的点.根据牛顿运动定律得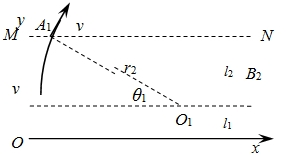
qvB2=m
,v2 r2
代入数据解得r2=
=0.4mmv qB2
如右图几何关系可知sinθ1=
=0.5l2 r2
A1点的横坐标为
x1=r2-r2cosθ1=(0.4-0.2
)m3
下图中,若A2为最右边点,则A2为轨迹与边界MN的切点.过C1点作速度方向的垂线,O1为带电粒子在磁场B1中运动的圆心,O2为在磁场B2中运动的圆心.由几何知识可得:
O2C2=r2-(l1+l2)=0.1m
sinθ2=
=0.5,即θ2=30°,l1+O2C2 r2
由此可得A2点的横坐标x2为:x2=r1(1-cosθ2)+r2cosθ2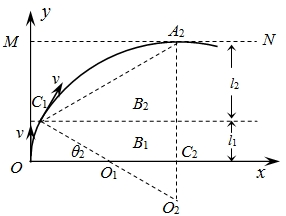
由几何知识可知此时r1=0.2m
解得:x2=(0.2+0.3
)m3
(3)粒子轨迹与MN相切时,粒子在磁场中运动轨迹最长,时间也最长.由于粒子在磁场中做匀速圆周运动,且轨迹左右对称,则粒子在磁场B1中的运动时间为t1=2×
=θ2r1 v
×10-7sπ 3
粒子在磁场B2中的运动时间为:t2=2
=(
-θ2)r2π 2 v
×10-7s4π 3
带电粒子在磁场中运动的最长时间为tmax=t1+t2=5.2×10-7s
随着磁场B1逐渐增大,带电粒子在磁场中的运动时间先增大后减小,当B1达到最大值时,运动半径为r1min=
=0.08m<0.1mmv qBmax
此时带电粒子在B1磁场中运动的时间为t1/=
=πm qB1
×10-7s2π 5
若B1=0时,带电粒子在B1、B2磁场中运动的总时间为t2/=
+l1 v
=1.55×10-7s>t1/θ1m qB1
所以带电粒子在磁场中的最短运动时间为
t1′=1.26×10-7s
答:(1)0~0.8s时间内B1的值小于0.4T,粒子运动半径大于l1,这段时间从O发射的粒子将进入磁感应强度B2的区域;
(2)带电粒子打在磁场上边界MN上的x坐标范围是(0.4-0.2
)m到x2=(0.2+0.33
)m之间;3
(3)在MN以下整个磁场区域内,单个带电粒子运动的最长时间和最短时间分别是5.2×10-7s,1.26×10-7s