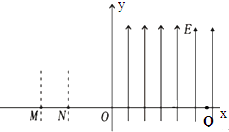
如图所示,直角坐标系的ox轴水平,oy轴竖直;M点坐标为(-0.3m,0)、N点坐标为(-0.2m,0);在-0.3m≤X≤-0.2m的长条形范围内存在竖直方向的匀强电场E0;在X≥0的范围内存在竖直向上的匀强电场,场强为E=20N/C;在第一象限的某处有一圆形的匀强磁场区,磁场方向垂直纸面向外,磁感应强度B=2.5T.有一带电量q=+1.0×10-4C、质量m=2×10-4kg的微粒以v0=0.5m/s的速度从M点沿着x轴正方向飞入电场,恰好垂直经过y轴上的P点(图中未画出,yP>0),而后微粒经过第一象限某处的圆形磁场区,击中x轴上的Q点,速度方向与x轴正方向夹角为60°.g取10m/s2.求:
(1)场强E0的大小和方向;
(2)P点的坐标及圆形磁场区的最小半径r;
(3)微粒从进入最小圆形磁场区到击中Q点的运动时间(可以用根号及π等表示)
(1)E0方向向上---①
微粒穿过MN、NO区的时间分别为t1、t2,则
t1=
-------②MN v0
t2=
-------③NO v0
过MN区加速度a竖直向上,速度变化量大小为△v:a=
---④△v t1
过NO区:g=
-------⑤△v t2
且qE0-mg=ma------⑥
由①~⑥得E0=60N/C-------⑦
(2)过N界偏移y1=
at12------⑧1 2
y2=
gt22----⑨1 2
则yP=y1+y2=1.2m----⑩
故P点的坐标为:(0,1.2m)
由qE=mg------(11)
得微粒飞入磁场做速度为v0的匀速圆周运动,设轨道半径为R,
由qv0B=m
-----(12)v02 R
R=
=0.4m--------------(13)mv0 qB
由几何关系得最小磁场区半径r=
=AC 2
=0.2m----(14)R 2
(3)磁场中运动时间t3=
T=1 6
---(15)πm 3qB
C~Q时间t4=
---(16)CQ v0
由几何关系得CQ=
m-----(17)2 3 3
t=t3+t4=
s-------(18)4π+20 3 15
答:(1)场强E0的大小为60N/C,方向向上;
(2)P点的坐标为(0,1.2m),圆形磁场区的最小半径为0.2m;
(3)微粒从进入最小圆形磁场区到击中Q点的运动时间
s4π+20 3 15

