问题
填空题
在△ABC中,点D、E、F顺次在边AB、BC、CA上,设AD=p•AB,BE=q•BC,CF=r•CA,其中p、q、r是正数,且使p+q+r=
|
答案
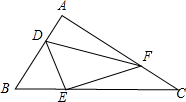
如图:
∵AD=p•AB,BE=q•BC,CF=r•CA,
∴S△ADF=(1-r)•p•S△ABC,S△BDE=(1-q)•r•S△ABC,S△EFC=(1-p)•q•S△ABC,
∴S△DEF=S△ABC-S△ADF-S△BDE-S△EFC=[1-(1-r)•p-(1-q)•r-(1-p)•q]•S△ABC=[1-(p+q+r)+(pr+qy+pq)]•S△ABC,
∵(p+q+r)2=(p2+q2+r2)+2(pr+qr+pq),p+q+r=
,p2+q2+r2=2 3
,2 5
∴pr+qr+pq=
[(p+q+r)2-(p2+q2+r2)]=1 2
,1 45
∴S△DEF=(1-
+2 3
)•S△ABC=1 45
S△ABC,16 45
∴S△DEF:S△ABC=16:45.
故答案为:16:45.