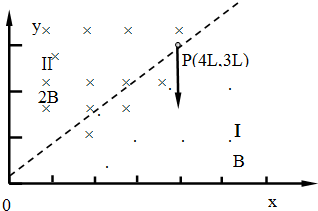
如图,在空间中有一坐标系xOy,其第一象限内充满着两个匀强磁场区域I和II,直线OP是它们的边界,区域I中的磁感应强度为B,方向垂直纸面向外;区域II中的磁感应强度为2B,方向垂直纸面向内,边界上的P点坐标为(4L,3L).一质量为m电荷量为q的带正粒子从P点平行于y轴负方向射入区域I,经过一段时间后,粒子恰好经过原点O,忽略粒子重力,已知sin37°=0.6,cos37°=0.8.求:
(1)粒子从P点运动到O点的时间为多少?
(2)粒子的速度大小是多少?
(1)设粒子的入射速度为v,用R1,R2,T1,T2分别表示粒子在磁场I区和II区中运动的轨道半径和周期.则
 qvB=m
qvB=mv2 R1
qv2B=mv2 R2
周期分别为 T1=
=2πR1 v
,T2=2πm qB
=2πR2 v πm qB
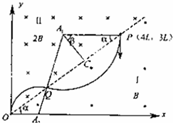
粒子先在磁场I区中做顺时针的圆周运动,后在磁场II区中做逆时针的圆周运动,然后从O点射出,这样粒子从P点运动到O点所用的时间最短.
粒子运动轨迹如图所示.tanα=
=0.753L 4L
得α=37°,α+β=90°
粒子在磁场I区和II区中的运动时间分别为t1=
•T1,t2=2β 360°
•T22β 360°
粒子从P点运动到O点的时间至少为t=n(t1+t2)(n=1,2,3,…)
由以上各式解得t=n
,(n=1、2,3,…) 53πm 60qB
(2)粒子的速度大小满足一定条件时,粒子先在磁场I区中运动,后在磁场II区中运动,然后又重复前面的运动,直到经过原点O.这样粒子经过n个周期性的运动到过O点,每个周期的运动情况相同,粒子在一个周期内的位移为S=
=OP n
=(4L)2+(3L)2 n
(n=1、2,3,…) 5L n
粒子每次在磁场I区中运动的位移为S1=
S=R1 R1+R2
S2 3
由图中几何关系可知
=cosαS1 2 R1
由以上各式解得粒子的速度大小为v=
(n=1、2,3,…)25qBL 12nm
答:
(1)粒子从P点运动到O点的时间为n
,(n=1、2,3,…) 53πm 60qB
(2)粒子的速度大小是
,(n=1、2,3,…)25qBL 12nm
