问题
填空题
设关于x的不等式组
|
答案
由条件|x+1|<2得-3<x<1.由分析知,不等式x2+2ax+3-a<0的解的集合的区间长度有着限制,
也即方程x2+2ax+3-a=0的解的集合的区间长度有着限制,设f(x)=x2+2ax+3-a
则有f(0.5)=3.25>0,结合-3<x<1和抛物线的图象,
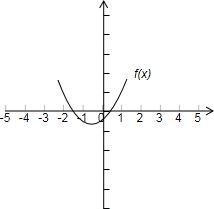
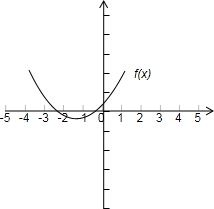
得
或f(0)<0 f(-1)<0 f(-2)>0 f(0)>0 f(-1)<0 f(-2)>0
解之得,实数a的取值范围为(
,3]7 5
故填(
,3].7 5