问题
问答题
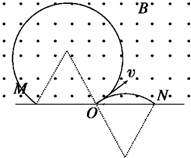
如图所示,直线MN上方有磁感应强度为B=5×10-4T的匀强磁场.正、负电子(质量相同、电量相同,电性相反)同时从同一点O以与MN成30°角的同样速度v=8×106m/s射入磁场(电子质量为m=9×10-31Kg,电荷量为e=1.6×10-19C).求:
(1)定性地画出正负电子在磁场中的运动轨迹;
(2)电子在磁场中做圆周运动的半径和周期;
(3)它们从磁场中射出位置之间的距离以及射出的时间差.

答案
(1)由左手定则判断正负粒子的洛伦兹力方向,画出其轨迹如图;
(2)根据牛顿第二定律:evB=mv2 R
得:R=
=9×10-2mmv qB
T=2πR v
得:T=
=2πm qB
×10-8s9π 4
由公式轨道半径R=
和周期T=mv qB
知,它们的半径和周期是相同的.只是偏转方向相反.先确定圆心,画轨迹,后由几何关系求半径,由对称性知:射入、射出点和圆心恰好组成正三角形.2πm qB
所以两个射出点相距2R=
=0.18m2mv eB
由图还可看出,经历时间相差为:
=2T 3
=4πm 3eB
×10-8s3π 2
答:(1)定性地画出正负电子在磁场中的运动轨迹如图;
(2)电子在磁场中做圆周运动的半径为0.09m,周期为
×10-8s;9π 4
(3)它们从磁场中射出位置之间的距离0.18m,射出的时间差为
×10-8s.3π 2