如图所示，在xoy平面内第二象限存在水平向左的匀强电场，场强为E，第一象限和第四象限存在垂直纸面向里的匀强磁场．有一质量为m，电荷量为e的电子，从x轴上的P点以某一初速度垂直于x轴进入电场，而后经过y轴上A点进入右侧磁场做圆周运动，轨迹交于x轴上的C点，电子在C点的速度垂直于x轴指向y轴负方向，继续运动从y轴上的某点离开磁场．已知P点坐标（-L，0），A点坐标（0，2L），忽略电子所受重力．求：
（1）电子从P点进入电场时的初速度大小；
（2）匀强磁场的磁感应强度B的大小；
（3）电子从P点进入电场到离开磁场所经历的时间．
（1）电子在电场中做类平抛运动，
在x轴方向上做初速度为零的匀加速直线运动，
由牛顿第二定律得：eE=ma，
位移：x=L=
at12，1 2
解得：t1=
；2mL eE
在y轴方向上做匀速直线运动，
位移：y=2L=v0t1，
解得：v0=
；2eEL m
（2）设电子经过A点时速度的大小为v，
x轴方向分速度：vx=at=
，2eEL m
y轴方向分速度：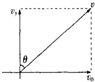
vy=v0=
，2eEL m
电子进入磁场时的速度：v=
=vx2+vy2
v0=22
，eEL m
设v的方向与y轴夹角为θ，
则有：cosθ=
=vy v
，θ=450．2 2
电子在磁场中做匀速圆周运动，如图所示，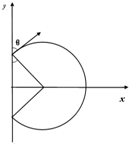
由牛顿第二定律得：evB=m
，v2 R
由图中几何关系可知，R=
=22L cosθ
L，2
解得：B=
；mE 2eL
（3）电子在磁场中做匀速圆周运动的周期：T=
，2πR v
解得：T=
=2π2πm eB
，2mL eE
电子在磁场中运动的时间为t2，由图中几何关系可知电子转过的圆心角为
．3π 2
电子在匀强磁场中的运动时间：t2=
T=3 4 3π 2
，2mL eE
电子在电场中运动的时间：t1=
，2mL eE
电子的运动时间：t=t1+t2=
+2mL eE 3π 2
=2mL eE 3π+2 2
；2mL eE
答：（1）电子从P点进入电场时的初速度大小为
；2eEL m
（2）匀强磁场的磁感应强度B的大小为
；mE 2eL
（3）电子从P点进入电场到离开磁场所经历的时间为3π+2 2
．2mL eE