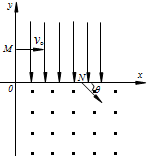
【选做题】如图所示,在平面直角坐标系xoy中,第一象限存在沿y轴负方向的匀强电场,第四象限存在垂直纸面向外的匀强磁场,磁感应强度B=
.一质量为m、电荷量为q的带正电粒子从y轴正半轴上的M点以速度v0垂直于y轴射入电场,经x轴上N点与x轴正方向成θ=60°角射入匀强磁场中,最后从y轴负半轴某一点P射出,已知M点坐标为(0,3L),不计粒子重力,求:mv0 qL
(1)匀强电场的电场强度和粒子到N点的速度;
(2)粒子在磁场中运动的轨道半径和粒子打在P点的坐标;
(3)粒子从进入M点运动到P点所用的总时间.
(1)粒子在电场中运动时做类平抛运动:水平方向匀速直线,竖直方向做初速度为零的匀加速直线运动,合速度与分速度的关系如图:
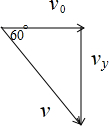
tan60°=
则vy=vy vx
v03
vy=at=
=qEt m
v0…①3
且竖直方向做初速度为零的匀加速直线运动:OM=
at2=1 2
t2=3L…②qE 2m
由①②解得:E=m v 20 2qL
vN=
=2v0
+v 2x v 2y
(2)粒子在电场中运动,竖直方向的平均速度:
=. vy
=0+vy 2
v0,3 2
所以竖直方向的位移:3L=
v0t…③3 2
水平方向的位移:x=0N=v0t…④
由③④解得:x=2
L3
由洛伦兹力提供向心力得:qBvN=mvN2 R
则R=
=2LmvN qB
粒子在磁场中的运动轨迹如图: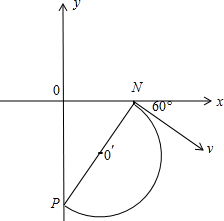
由图可以看出PN与x轴方向的30°,由于ON等于2
L,3
则:PN=
=4LON cos30°
PN距离恰好为半径的两倍,说明粒子正好从NP直径出第四象限
即打在y轴负半轴的坐标(0,-2L)
(3)粒子在电场中做类平抛运动,水平位移x=0N=v0t=2
L,3
解得:t=2
L3 v0
粒子在磁场中运动轨迹为半圆,所需的时间:t2=
=πR vN
=π2L 2v0 πL v0
所以粒子的运动总时间为t总=2
L+πL3 v0
答:(1)匀强电场的电场强度为
,粒子到N点的速度为2v0;m v 20 2qL
(2)粒子在磁场中运动的轨道半径为2L,粒子打在P点的坐标为(0,-2L);
(3)粒子从进入M点运动到P点所用的总时间为
.2
L+πL3 v0
