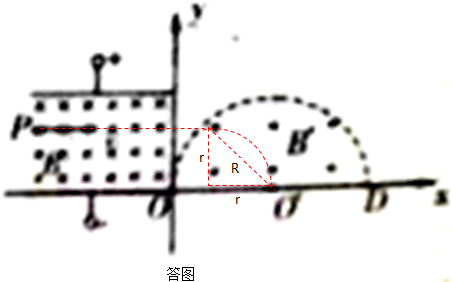
如图所示，在xoy坐标系第一象限内有一半径为R的半圆形匀强磁场，圆心为O′，在第二象限内有一平行板电容器，其下极板恰好与x轴重合，平行板右端与y轴相齐．已知平行板内存在相互正交的匀强电场和匀强磁场，电场的场强为E，磁场的磁感应强度为B．有一质量为m，带电量为q的带电粒子（其重力不计），沿平行于x轴的方向从P点射入电容器，且恰好作直线运动，后又进入第一象限的半圆形磁场，最后由O′点垂直x轴射出．求：

（1）带电粒子的速度v；

（2）半圆形磁场的磁感应强度B′．