问题
问答题
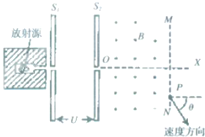
容器内某放射性原子在衰变生成新核过程中放出一个粒子,设该粒子的质量为m,电荷量为q,设粒子从放射源出进入平行极板S1窄缝时初速度近似为零,平板电极S1和S2间的电势差为U,粒子经电场加速后,沿OX方向进入磁感应强度为B、方向垂直纸面向外的有界匀强磁场,OX垂直平板电极S2,当粒子从P点离开磁场右边界MN时,其速度方向与OX方位的夹角θ=60°,如图所示,整个装置处于真空中.
(1)求粒子在磁场中沿圆弧运动的轨道半径R;
(2)求粒子在磁场中运动所用时间t;
(3)若撤去磁场,并在原磁场区域加上平行于极板方向的匀强电场,使粒子仍然从边界MN上岸原方向出射,求所加匀强电场的电场强度大小.
答案
(1)设粒子离开电场时速度为v0,对加速过程有:
qU=
mv02…①1 2
粒子在磁场中有:
qv0B=m
…②v02 R
由②、③得:
R=m qB
=2qU m 1 B
…③2mU q
(2)粒子做圆周运动的回旋周期
T=
=2πR v0
…④2πm qB
粒子在磁场中运动时间为:
t1=
T…⑤1 6
由④⑤得:
t1=
…⑥πm 3qB
(3)粒子进入新电场中做类平抛运动
Rsinθ=v0t2…⑦
vy=
t2…⑧qE m
在P点处,有:
vy=v0tanθ… ⑨
联立上述方程得:
E=2B
…⑩2qU m
答:(1)粒子在磁场中沿圆弧运动的轨道半径R=1 B
;2mU q
(2)粒子在磁场中运动所用时间t=
;πm 3qB
(3)若撤去磁场,并在原磁场区域加上平行于极板方向的匀强电场,使粒子仍然从边界MN上岸原方向出射,所加匀强电场的电场强度大小2B
.2qU m