如图所示,水平放置的平行金属板A和D间的距离为d,金属板长为L=
d,两板间所加电压为U,D板的右侧边缘恰好是倾斜挡板NM上的一个小孔K,NM与水平挡板NP成60°角,且挡板足够长,K与N间的距离为KN=a.现有一质量为m、电荷量为q的带正电的粒子,从A、D的中点O沿平行于金属板方向OO'以某一速度射入,不计粒子的重力.该粒子穿过金属板后恰好穿3 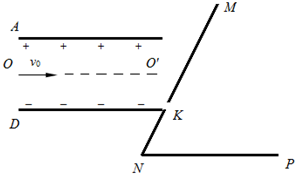 过小孔K:
过小孔K:
(1)求该粒子从O点射入时的速度大小v0;
(2)若两档板所夹的整个区域存在一垂直纸面向外的匀强磁场,粒子经过磁场偏转后能垂直打在水平挡板NP上,求该磁场的磁感应强度的大小B0;
(3)若磁场方向变为垂直纸面向里,且只存在于两档板所夹间的某一区域内,同样使该粒子经过磁场偏转后能垂直打在水平挡板NP上(之前与挡板没有碰撞),求满足条件的磁感应强度的最小值Bmin.
(1)粒子在电场中做类平抛运动:L=v0t
=d 2
at21 2
a=qU dm
代入:L=
d3
可得:v0=3qU m
(2)射入的粒子在进入K时竖直方向的分速度为vy
水平方向:L=
d=v0t3
竖直方向:
=d 2
tvy 2
可得:tanθ=
=vy v0
即:θ=30°,3 3
粒子到达K点时速度为:v=2qU m
由几何关系可得:粒子圆周运动半径为r=a
且满足:qB0v=mv2 r
可得:B0=2 a Um q
(3)磁场反向,如图,粒子从K点入射后做匀速直线运动从D点开始进入磁场,根据对称性,需偏转300°后从E点射出,做匀速直线运动垂直打到NP挡板上.
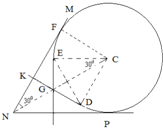
根据:Bqv=m
可得:B=v2 r mv qr
要使B最小,则需使半径r最大,临界情况是轨迹刚好和挡板相切
由几何关系可得:
r=a+r3
可得:r=a
-13
解得:Bmin=2(
-1)3 a Um q
答:(1)该粒子从O点射入时的速度大小为
;3qU m
(2)该磁场的磁感应强度的大小为2 a
;Um q
(3)满足条件的磁感应强度的最小值为2(
-1)3 a
.Um q