问题
问答题
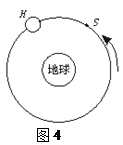
宇航员乘太空穿梭机，去修理位于离地球表面6.0×105 m的圆形轨道上的哈勃太空望远镜H，机组人员使穿梭机S进入与H相同的轨道并关闭推动火箭，而望远镜则在穿梭机前方数千米处，如图4所示，设G为引力常量，ME为地球质量.（已知地球半径为6.4×106 m）
（1）在穿梭机内，一质量为70 kg的太空人的视重是多少？
（2）①计算轨道上的重力加速度的值；
②计算穿梭机在轨道上的速率和周期;
（3）穿梭机须首先进入半径较小的轨道，才有较大的角速度追上望远镜，试判断穿梭机要进入较低轨道时应在原轨道上加速还是减速？说明理由．
答案
（1）视重为零；（2）①8.2 m/s2，②7.6 km/s；（3）要进入较低轨道应减小其原有速度。
（1）穿梭机内的人处于完全失重状态，视重为零。
（2）①由万有引力定律得：
mg′=G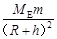
，
即g′="8.2" m/s2
②由万有引力定律得：
G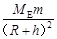= m（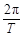
）2（R+h）
即T=5.8×103 s
则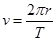
得：
v="7.6" km/s，
（3）要进入较低轨道应减小其原有速度。因为先减小其原有速度，其所受地球的引力大于其需要的向心力，故穿梭机做向心运动从而进入半径较小的轨道，这样万有引力做正功，从而使穿梭机获得较大的角速度，到达预定位置时，再使其加速而做离心运动回来原来的轨道，以赶上哈勃太空望远镜H，这样才能真正“追上”哈勃望远镜。