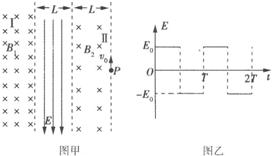
如图甲所示,I、Ⅱ两区是垂直于纸面的匀强磁场,磁场的边界相互平行,I区的磁感应强度为B1,磁场宽度足够大.Ⅱ区的磁感应强度为B2,磁场宽度为L.两磁场之间匀强电场的宽度为L.一质量为m、电荷量为+q、重力不计的粒子,从Ⅱ区右边界的P点以平行于边界且与磁场垂直的初速度v0开始运动,以此作为计时起点,竖直向下为电场的正方向,电场随时间做周期性变化的规律如图乙所示.粒子离开Ⅱ区进入电场时,速度恰好与电场方向垂直.再经过一段时间,粒子恰又回到P点,如此循环,粒子循环运动一周,电场恰好变化一个周期.已知sin37°=0.6,cos37°=0.8.
(1)请用E0及已知量表示粒子第一次穿越电场时沿电场方向的偏移量;
(2)若E0=,要实现上述循环,求B1的大小;
(3)在满足(2)问的条件下,求电场变化的周期.
(1)粒子在电场中运动的时间 t= ①
沿电场方向的位移 y=at2 ②
y= ③
(2)由题意,粒子离开电场时沿电场方向的速度
vy=at=•=v0 ④
故粒子进入Ⅰ区磁场时,速度大小 v===v0 ⑤
粒子在电场中沿y方向的位移 y=at2=t2=L ⑥
粒子在Ⅰ区做圆周运动的圆心必须在过P点且与电场垂直的虚线上才能满足要求,由几何关系,有:
= ⑦
得:R=L ⑧
由R=得:B1== ⑨
(3)粒子在Ⅱ区转四分之一圆弧所用的时间 t1=•=
粒子在Ⅰ区转37°所用的时间 t2=•=
电场变化的周期 T=2(t1+t+t2)=2×(++)=++
答:
(1)粒子第一次穿越电场时沿电场方向的偏移量为;
(2)B1的大小为;
(3)电场变化的周期为++.


