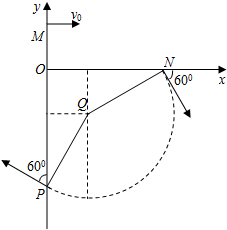
平面直角坐标系xOy中,第1象限存在沿y轴负方向的匀强电场,第Ⅳ象限存在垂直于坐标平面向外的匀强磁场,磁感应强度大小为B.一质量为m、电荷量为q的带正电的粒子从y轴正半轴上的M点以速度v0垂直于y轴射入电场,经x轴上的N点与x轴正方向成60°角射入磁场,最后从y轴负半轴上的P点与y轴正方向成600角射出磁场,如图所示.不计粒子重力,求
(1)粒子在磁场中运动的轨道半径R;
(2)粒子从M点运动到P点的总时间t;
(3)匀强电场的场强大小E.
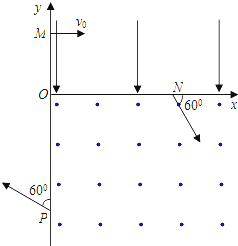
(1)设粒子过N点时的速度为v,根据平抛运动的速度关系
v=
①v0 cos60°
分别过N、P点作速度方向的垂线,相交于Q点,则Q是粒子在磁场中做匀速圆周运动的圆心,根据牛顿第二定律 qvB=
②mv2 R
联立①②解得轨道半径 R=
③2mv0 qB
(2)设粒子在电场中运动的时间为t1,有 ON=v0t1 ④
由几何关系得 ON=Rsin30°+Rcos30°⑤
联立③④⑤解得 t1=
⑥(1+
)m3 qB
粒子在磁场中做匀速圆周运动的周期 T=
⑦2πm qB
由几何关系知∠NQP=150°,设粒子在磁场中运动的时间为t2
t2=
T⑧150° 360°
联立⑦⑧解得 t2=
⑨5πm 6qB
故粒子从M点运动到P点的总时间 t=t1+t2=(1+
+3
)5π 6
⑩m qB
(3)粒子在电场中做类平抛运动,设加速度为a,运动时间为t
由牛顿第二定律:qE=ma (11)
设沿电场方向的分速度为vy,
vy=at(12)
粒子在电场中x轴方向做匀速运动,由图根据粒子在磁场中的运动轨迹可以得出:
粒子在x轴方向的位移:Rsin30°+Rcos30°=v0t (13)
又:vy=v0tan60°(14)
联立(11)(12)(13)(14)可以解得E=(3-
)v0B3 2
答:(1)粒子在磁场中运动的轨道半径为2mv0 qB
(2)粒子从M点运动到P点的总时间为(1+
+3
)5π 6 m qB
(3)匀强电场的场强大小为(3-
)v0B3 2