如图1所示的装置是由加速器、电场偏转器和磁场偏转器构成.加速器两板a、b间加图2所示变化电压uab,水平放置的电场偏转器两板间加恒定电压U0,极板长度为l,板间距离为d,磁场偏转器中分布着垂直纸面向里的左右有界、上下无界的匀强磁场B,磁场的宽度为D.许多质量为m、带电量为+q的粒子从静止开始,经过加速器加速后从与电场偏转器上板距离为
的位置水平射入.已知:U0=1000V,B=2d 3
T,粒子的比荷3 6
=8×107C/kg,粒子在加速器中运动时间远小于Uab的周期,粒子经电场偏转后沿竖直方向的位移为y,速度方向与水平方向的夹角为θ,y与tanθ的关系图象如图3所示.不考虑粒子受到的重力.q m
(1)求电场偏转器极板间距离d和极板长度l;
(2)为使从电场偏转器下极板边缘飞出的粒子不从磁场区域右侧飞出,求磁场宽度D的最小值,并求出该粒子在两个偏转器中运动的总时间;
(3)求哪些时刻进入加速器的粒子能够进入磁场区域.
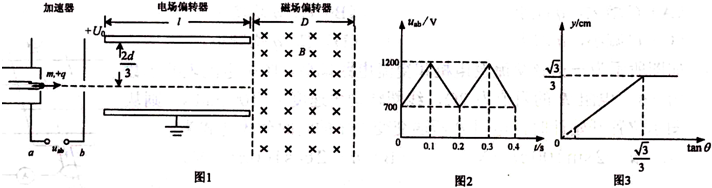
由图(3)可知,当tanθ=
时,对应粒子恰好从下板边缘飞出进入磁场,即:3 3
=d 3
d=3 3
cm3
对能够飞出电场的粒子而言:y=
tanθl 2
代入数据可的:l=2cm
(2)设从下极板边缘飞出的粒子进入电场偏转器时的速度为v0,进入磁场后恰好不从磁场右侧飞出,此时磁场宽度为D0
y=
at21 2
y=
F=qE a=d 3
E=F m
t=U0 d l v0
联立并代入数据得:v0=4×105m/s
设粒子在磁场中运动的速度为v,半径为R
qvB=mv2 R
v=v0 cosθ
D0=R+Rsin30°
联立并代入数据得:D≥0.03m
该粒子在磁场中运动周期T=2πm qB
代入数据得:t=
×10-2s2
π+33 6
(3)对从下板边缘飞出的粒子,设它进入加速度场时加速度电压为U,由(2)问得:v0=4×105m/s
qU=
mv021 2
得:U=U0=1000V
为使粒子能够进入磁场区域,则必须加速电压U≥1000V
由图可知,进入时刻t应满足:
(0.2n+0.06)s≤t≤(0.2n+0.14)s(n=0,1,2,…)
答:(1)电场偏转器极板间距离d为
cm,极板长度l为2cm;3
(2)为使从电场偏转器下极板边缘飞出的粒子不从磁场区域右侧飞出,磁场宽度D的最小值为0.03m,该粒子在两个偏转器中运动的总时间
×10-2s;2
π+33 6
(3)(0.2n+0.06)s≤t≤(0.2n+0.14)s时刻进入加速器的粒子能够进入磁场区域.
