问题
问答题
在水平面上有一沿y轴放置的长为L=1m的细玻璃管，在管底有光滑绝缘的带正电的小球．在第一象限中存在磁感应强度为B＝1T的匀强磁场，方向如图所示。已知管沿x轴以v＝1m/s的速度匀速向右运动，带电小球的荷质比为
，不计小球的重力。求：
（1）带电小球从管底到飞出管口时所用的时间是多少？
（2）带电小球离开磁场时的位置到坐标原点的距离是多少？
（3）带电小球从刚离开管口后到离开磁场时所用的时间是多少？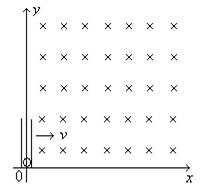
答案
（1）t=2s
（2）
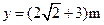
（3）
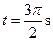
小球在离开管之前随管向右以v平动，同时沿管壁做初速度为零的匀加速运动。
（1）设小球的质量为m，加速度为a，受到的洛伦兹力为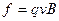
由牛顿第二定律有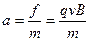
①
而
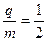②
小球飞出管口所有时间为t，则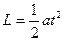
③
联立①②③并代入数据解得：t="2s" ④
（2）小球飞出管口时沿管壁方向的速度为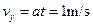
⑤
飞出时的合速度为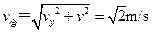
⑥
合速度的方向与x轴夹角为θ，
，θ＝45°⑦
又设小球以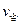
在磁场中作圆周运动的半径为r，由牛顿第二定律有
⑧
联立②⑥⑧式并代入数据解得：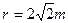
⑨
又小球飞出管口时，在x方向上移动的距离为
。
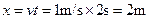如答图所示，由几何知识可知，小球在磁场中运动的圆心在y轴上（图中O点），圆弧所对应的圆心角为135°。
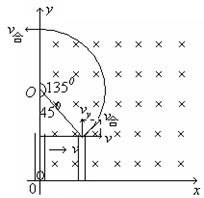
所以，带电小球离开磁场时离坐标原点的距离为
。
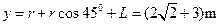（3）小球在磁场中做匀速圆周运动的周期为
，
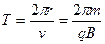代入数据解得：T=4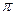
s。
所以，带电小球从离开管口到离开磁场所用的时间是：
。
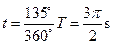