如图a所示,水平直线MN下方有竖直向下的匀强电场,现将一重力不计、比荷
=106C/kg的负电荷于电场中的.点由静止释放,经过q m
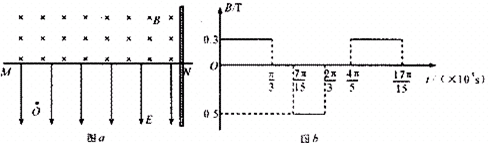
×10-5s后电荷以v0=1.5X104m/sS的速度通过MN进人其上方的均匀磁场,磁场与纸面垂直,磁感应强度B按图b所示规律周期性变化.图中以垂直纸面向里为正,电荷通过MN时为t=0时刻.求:π 15
(1)匀强电场的电场强度E及O点与直线MN之间的距离;
(2)如果在O点正右方d=68cm处有一垂直于MN的足够大的挡板,求电荷从O点出发运动到挡板的时间.
(1)电荷在电场中做匀减速直线运动,设其在电场中运动的时间为tE,
根据动量定理可知,mv0=qEtE
解得,E=
=mvo qtE
×104N/C=7.2×103N/C4.5 2π
O点与直线MN之间的距离d=
a1 2
=t 2E
cm=1.57cmπ 2
(2)当磁场垂直纸面向里时,
电荷运动的半径r1=
=mvo qB1
m=5cm10-6×1.5×104 0.3
周期T1=
=2xm qB1
8=2π×10-6 0.3
×10-6S2π 3
当磁场垂直纸面向外时,
电荷运动的半径r2=
=mvo qB2
m=3cm10-6×1.5×104 0.5
周期T2=
=2πm qB2
=2πm qB2
5=2π×10-6 0.5
×10-582π 5
根据电荷的运动情况可知,电荷到达挡板前运动的完整周期数为15个,即沿ON运动的距离S=15△d=60cm,最后8cm的距离
如图所示,r1+r1cosa=d-S
解得cosα=0.6则α=53°
故电荷运动的总时间
T=tk+15TB+
T1-1 2
T153 360
=(12+
)x×10-5S=3.86×10-4S163 540
答:(1)匀强电场的电场强度7.2×103N/C及O点与直线MN之间的距离1.57cm;
(2)如果在O点正右方d=68cm处有一垂直于MN的足够大的挡板,则电荷从O点出发运动到挡板的时间3.86×10-4s.
