问题
选择题
用边长相等的正多边形进行密铺，下列正多边形能和正八边形密铺的是（ ）
A．正三角形
B．正六边形
C．正五边形
D．正四边形
答案
正八边形的每个内角为180°-360°÷8=135°，
A、正三角形的每个内角60°，得135m+60n=360°，n=6-94m，显然m取任何正整数时，n不能得正整数，故不能铺满；
B、正六边形的每个内角是120度，得135m+120n=360°，n=3-98m，显然m取任何正整数时，n不能得正整数，故不能铺满．
C、正五边形每个内角是180°-360°÷5=108°，得108m+135n=360°，m取任何正整数时，n不能得正整数，故不能铺满；
D、正四边形的每个内角是90°，得90°+2×135°=360°，所以能铺满；
故选D．
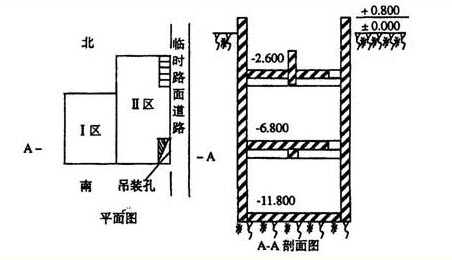设备布置和设计要求是： ①-2.600层I区安装冷却塔及其水池。②-6.800层I区安装燃油供热锅炉、Ⅱ区北侧安装换热器，南侧安装各类水泵。③-11.800层I区为变配电所、Ⅱ区北侧安装离心冷水机组，南侧安装柴油发电机组。④动力中心设有通风排气和照明系统，在-11.800层地面下有集水坑。各层吊装孔在设备吊装结束后加盖，达到楼面强度，并做防渗漏措施。⑤每种设备均有多台，设备布置紧凑，周界通道有限。 安装开工时，工程设备均已到达现场仓库。所有工程设备均需用站位于吊装孔边临时道路的汽车吊(40t)，吊运至设备所在平面层，经水平拖运才能就位。 问题