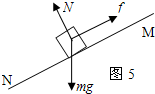
如图所示，在倾角为θ，用绝缘材料制成的斜面上，一个质量为m，带电量为+q小滑块，它与斜面间的动摩擦因数为µ（µ＜tgθ）．整个装置处于方向垂直斜面向上，磁感应强度为B的匀强磁场中．若小滑块由A点静止释放，到达B点时刚好能做直线运动．已知斜面足够大，滑块电量不变，A、B两点高度差为H．
求：（1）试根据小滑块的受力特点，分析小滑块经过b点后的运动情况；
（2）小滑块作直线运动时的速度方向与斜面边线MN的夹角（用三角函数表示）；
（3）小滑块从A运动到B的过程中，滑动摩擦力所做的功．
（1）滑块在斜面上a点时受力分析如图5所示：
小滑块受到的支持力为N=mgcosθ，
释放后，受到的摩擦力大小为f=μmgcosθ，
因重力沿斜面向下的分力F1=mgsinθ＞f（依µ＜tgθ可知），
小滑块将向下运动，此时受到的洛伦兹力为f洛=qvB
当滑块在斜面上b点作直线运动时，速度方向不变，所以洛仑兹力方向不变；而重力的分力F1的大小（=mgsinθ）、方向（平行于斜面的边线MN向下）不变，摩擦力f大小（=μmgcosθ）、方向（与运动方向相反）也不变，所以洛仑兹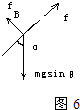
力的大小也不变，物块将做匀速直线运动（否则不能作直线运动）．
（2）在b点时，从上往下正对斜面所在平面来看（即俯视图，此时磁场方向垂直纸面向外），滑块的受力如图6所示，
设运动方向与MN夹角（∵F1∥MN，即v与F1的夹角）为α
则：cosα=
=μcotθμmgcosθ mgsinθ
（3）由上分析知，小滑块通过b点后作匀速直线运动，受力平衡，所以：f2洛+f2=(mgsinθ)2
将f=μmgcosθ、f洛=qvB，代入得：v=mg qB sin2θ-μ2cos2θ
由A到B对物块用动能定理得：mgh+Wf=
mv21 2
解得：Wf=
(sin^-mghm3g2 2q2B2
答：（1）小滑块经过b点后物块将做匀速直线运动；
（2）小滑块作直线运动时的速度方向与斜面边线MN的夹角cosα=μcotθ；
（3）小滑块从A运动到B的过程中，滑动摩擦力所做的功为
(sin^-mgh．m3g2 2q2B2
