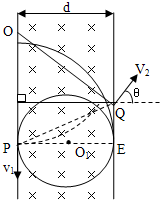
如图,有大量质量为m、电荷量为+q的带电粒子以等大速度从P点沿垂直于磁场的不同方向连续射入磁感应强度为B,磁场宽度为d的匀强磁场中,求解下列问题
(1)要使粒子不从右边界射出,粒子速度大小应满足的条件是什么?
(2)若粒子恰好不从右边界射出,这些粒子在磁场中所能到达区域的面积是多少?
(3)从P点垂直左边界进入磁场的粒子,能从右边界Q点射出,射出时速度方向改变θ角,求该粒子的速度大小和粒子的偏转距离(E、Q间的距离).
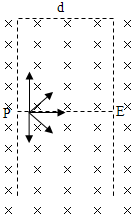
(1)根据题意画出粒子运动轨迹如图,
由牛顿第二定律,则有,qvB=m
…①v2 r
要使粒子不从右边界射出,应有:2r≤d…②
联立①②式解得:v≤qBd 2m
(2)若粒子恰好不从右边界射出,应有:2r1=d
此时粒子在磁场中所能到达的区域的面积为:S=
π1 2
+r 21
π(2r1)2=1 4
πd23 8
(3)设此时粒子速度为V2,轨迹半径为r2,由题意及几何知识得
∠Qo2P=θ
故有:r2=
…③d sinθ
由牛顿第二定律得:qv2B=
…④v 22 r2
联立③④式解得:v2=qBd msinθ
粒子偏转距离为:EQ=r2(1-cosθ)=
d.1-cosθ sinθ
答:(1)要使粒子不从右边界射出,粒子速度大小应满足的条件是v≤
;qBd 2m
(2)若粒子恰好不从右边界射出,这些粒子在磁场中所能到达区域的面积是
πd2;3 8
(3)该粒子的速度大小和粒子的偏转距离
d.1-cosθ sinθ