问题
问答题
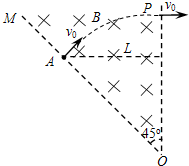
如图所示，在OM与OP之间无限大区域内存在着磁感应强度为B=2×10-3T的匀强磁场，磁场方向垂直纸面向内．一质量为m=6.4×10-27kg、电荷量为q=-3.2×10-19C的带电粒子从A点以速度v0垂直OM射入磁场，之后又垂直OP离开磁场．不计粒子重力，A点到OP边界的距离为L=0.2
m．求：2
（1）粒子的速度v0；
（2）粒子在磁场中运动的时间t；
（3）若要求粒子不能从OP边界射出，则粒子从A点垂直OM射入磁场的最大速度vm．
答案
（1）粒子做圆周运动有：Bqv0=m v 20 r
由几何知识知其半径为：r=L sin45°
解得：v0=BqL msin45°
代入数据得：v0=4×104m/s
（2）粒子在磁场中运动的时间：t=
rπ 4 v0
代入数据得：t=
×10-5sπ 4
（3）粒子不能从OP边界射出的临界情况为轨迹与OP相切，如图所示，设粒子此时的圆周运动半径为rm：
rm+
=rm sin45° L sin45°
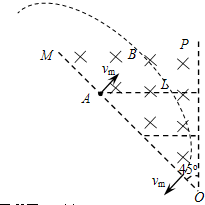粒子做圆周运动有：Bqvm=m v 2m rm
联立解得：vm=BqL m(1+sin45°)
代入数据得：vm=4（
-1）×104m/s2
答：（1）粒子的速度v0为4×104m/s；
（2）粒子在磁场中运动的时间t为
×10-5s；π 4
（3）若要求粒子不能从OP边界射出，则粒子从A点垂直OM射入磁场的最大速度vm为4（
-1）×104m/s．2
