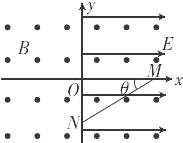
如图所示,坐标系xOy位于竖直平面内,空间中有沿水平方向、垂直纸而向外的匀强磁场,磁感应强度大小为B,在x>0的空间内有沿x轴正方向的匀强电场,电场强度大小为E.一带正电荷的小球从图中x轴上的M点沿着与水平方向成θ=30°角的斜向下的直线做匀速运动,进过y轴上的N点进入x<0的区域.要使小球进入x<0的区域后能在竖直面内做匀速圆周运动,需要在x<0的区域内另加一匀强电场.已知带电小球做圆周运动时通过y轴上的P点(P点未标出),重力加速度为g,求:
(1)小球运动的速度大小;
(2)在x<0的区域内所加匀强电场的电场强度的大小和方向;
(3)N点与P点间的距离.
(1)对小球在MN段的运动进行受力分析(如右图所示),
因小球做匀速直线运动,所以有:
qvBsin30°=qE
解得:小球运动的速度大小为 v=
.2E B
(2)在x<0的区域内,设所加的电场强度为E′,则由运动情况分析知,小球受的重力mg必与电场力qE′是一对平衡力,即有:
qE′=mg
又 mgtan30°=qE
故可得:E′=
E,其方向为竖直向上.3 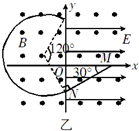
(3)小球在第二、三象限的磁场中做匀速圆周运动,根据牛顿第二定律,由洛伦兹力提供向心力,得:
qvB=mv2 R
则得,R=mv qB
画出轨迹,如图.设N、P间的距离为L,则结合几何关系,有:
L=2Rcos30°
联立解得:L=
.6E2 gB2
答:
(1)小球运动的速度大小为
;2E B
(2)在x<0的区域内所加匀强电场的电场强度的大小为
E,其方向为竖直向上.3
(3)N点与P点间的距离为
.6E2 gB2
