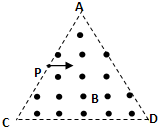
(A)如图所示,在边长为L=1m的等边三角形ACD区域内,存在磁感应强度为B=
T、方向垂直纸面向外的匀强磁场,现有一束比荷3 3
=102C/kg带正电粒子,从AC边中点P以平行于CD边的某一速度射入磁场,粒子的重力可忽略不计.q m
(1)若粒子进入磁场时的速度大小为v0=10m/s,求粒子在磁场中运动的轨道半径;
(2)若粒子能从AC边飞出磁场,求粒子在磁场中的运动时间;
(3)为使粒子能从CD边飞出磁场,粒子进入磁场时的速度大小应满足的条件?
(1)洛伦兹力提供向心力,则有:qvB=m
,v2 r
解之得:r=
=mv qB
×102m=0.1732m10 3 3
(2)从AC边出磁场如图

圆心角θ=4π 3
则有运动的时间为:t=
Tθ 2π
而T=
=2πr v 2πm qB
解之得:T=2π
×10-2s3
t=
×10-2s=7.25×10-2s4
π3 3
(3)设恰从CD边出磁场的轨迹半径为r1和r2.
根据几何关系,则有2r1=
sin60°L 2
解得:r1=
L3 8
由几何关系,有(r2-
L)2+(3 4
)2=3L 4
,r 22
解得:r2=
L3 2
由qvB=m
,v2 r
得v=
,qBr m
则v1=
=12.5m/s
qBL3 8m
又v2=
qBL3 2m
得v2=50m/s
即12.5m/s<v<50m/s
答:(1)若粒子进入磁场时的速度大小为v0=10m/s,则粒子在磁场中运动的轨道半径0.1732m;
(2)若粒子能从AC边飞出磁场,则粒子在磁场中的运动时间7.25×10-2s;
(3)为使粒子能从CD边飞出磁场,粒子进入磁场时的速度大小应满足的条件:12.5m/s<v<50m/s.
