问题
解答题
求函数f（x）=2x3+6x2-18x+3的极值．
答案
f′（x）=6x2+12x-18，令f′（x）=0，
解得x1=-3或x2=1．
当x∈（-3，1）时，f′（x）＜0；
当x∈（-∞，-3）或x∈（1，+∞）时，f′（x）＞0，
所以，当x=-3时，函数取得极大值f（-3）=57；当x=1时，函数取得极小值f（1）=-7．
搜题请搜索小程序“爱下问搜题”
求函数f（x）=2x3+6x2-18x+3的极值．
f′（x）=6x2+12x-18，令f′（x）=0，
解得x1=-3或x2=1．
当x∈（-3，1）时，f′（x）＜0；
当x∈（-∞，-3）或x∈（1，+∞）时，f′（x）＞0，
所以，当x=-3时，函数取得极大值f（-3）=57；当x=1时，函数取得极小值f（1）=-7．
材料一：
图一：商品供过于求 价格下跌 获得减少 缩小生产
扩大生产 获得增加 价格上涨 商品供不应求
 | |||
| |||
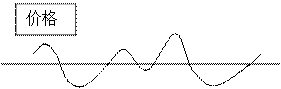
图二：
（1）图一和图二分别反映了什么经济现象？（2分）请简述材料一所含经济规律的名称和基本内容（3分）
材料二、2010年上半年，我国粮食、肉禽及其制品、蛋类的价格出现持续上涨，其中7月份猪肉价格继6月份短暂回落后再次反弹，指标创今年来新高。食品价格问题引起社会各方面普遍关注，已成为当前宏观经济运行的突出问题。对于当前某些产品出现供求偏紧、价格上涨问题，党中央、国务院高度重视，采取了一系列措施，一些问题正在得到缓解……。
（2）我国食品价格持续上涨的决定因素和直接因素分别是什么?食品价格上涨对我国农业生产和城乡低收入群众的生活带来哪些影响?（10分）