问题
解答题
已知平面向量a=(1,x),b=(2x+3,-x)(x∈R)。
(1)若a⊥b,求x的值;
(2)若a∥b,求|a-b|。
答案
解:(1)若a⊥b,则a·b=1×(2x+3)+x(-x)=0,
整理得x2-2x-3=0,
解得x=-1或x=3;
(2)若a∥b,则有1×(-x)-x(2x+3)=0,即x2+2x=0,
解得x=0或x=-2,
当x=0时,a=(1,0),b=(3,0),
所以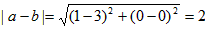
当x=-2时,a=(1,-2),b=(-1,2),
所以|a-b|=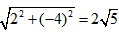 。
。
