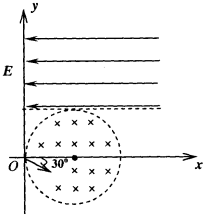
如图所示,真空中有以(r,0)为圆心,半径为r的圆形匀强磁场区域,磁场的磁感应强度大小为B,方向垂直于纸面向里,在y=r的虚线上方足够大的范围内,有方向水平向左的匀强电场,电场强度的大小为E.从O点向不同方向发射速率相同的质子,质子的运动轨迹均在纸面内,且质子在磁场中的偏转半径也为r,已知质子的电荷量为q,质量为m,不计重力、粒子间的相互作用力及阻力的作用.求:
(1)质子射入磁场时速度的大小:
(2)沿x轴正方向射入磁场的质子,到达y轴所需的时间;
(3)与x轴正方向成30°角(如图所示)射入的质子,从离开磁场到达y轴所需要的时间.
(1)质子射入磁场后有qvB=mv2 r
得到v=qBr m
(2)质子沿x轴正向射入磁场后经
圆弧后以速度v垂直于电场方向进入电场,1 4
质子在磁场中运动周期 T=
T=
=2πr v 2πm qB
在磁场中运动的时间为t1=
=T 4 πm 2qB
质子进入电场后做类平抛运动,沿电场方向运动r后到达y轴,因此有
r=
a1 2
,a=t 22 qE m
得到t2=2mr qE
故t=t1+t2=
+πm 2qB 2mr qE
(3)质子在磁场中转过120°角后从P点垂直于电场线进入电场,如图所示.P点距y轴的距离
x1=r+rsin30°=1.5r
又x1=
tqE 2m ′ 22
则质子到达y轴所需时间为t2′=3rm qE
答:(1)质子射入磁场时速度的大小为
.qBr m
(2)沿x轴正方向射入磁场的质子,到达y轴所需的时间为
+πm 2qB
.2mr qE
(3)与x轴正方向成30°角射入的质子,从离开磁场到达y轴所需要的时间为为
.3rm qE
