问题
问答题
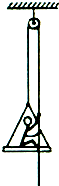
(A选做)宇航员登上某一星球并在该星球表面做实验,用一根不可伸缩的轻绳跨过轻质定滑轮,一端挂一吊椅,另一端被坐在吊椅上的宇航员拉住,如图所示.宇航员的质量m1=65kg,吊椅的质量m2=15kg,当宇航员与吊椅以a=1m/s2的加速度匀加速上升时,宇航员对吊椅的压力为l75N.(忽略定滑轮摩擦)
(1)求该星球表面的重力加速度g;
(2)若该星球的半径6×105,地球半径6.4×106,地球表面的重力加速度10m/s2,求该星球的平均密度与地球的平均密度之比.
答案
(1)设宇航员受到绳向上的拉力为F,由于跨过定滑轮的两段绳子拉力相等,吊椅受到绳的拉力也是F,对他和吊椅整体进行受力分析如图所示,则有:
2F-(m1+m2)g=(m1+m2)a
设吊椅对宇航员的支持力为FN,压力为FN′,根据牛顿第三定律得:FN=FN′.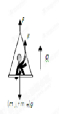
对宇航员,由牛顿第二定律得,F+FN-m1g=m1a
代入数据解得g=6m/s2.
(2)由星球密度ρ=
和M
πR34 3
=m′g得,GMm′ R2
该星球的平均密度与地球的平均密度之比
=ρ ρ0
,gR0 g0R
代入数值解得
=ρ ρ0
=0.64.16 25
答:(1)星球表面的重力加速度为6m/s2.
(2)该星球的平均密度与地球的平均密度之比0.64.
