问题
多选题
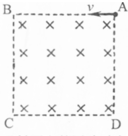
如图所示,正方形区域ABCD内存在方向垂直纸面向里的匀强磁场,三个完全相同的带电粒子a、b、c分别以大小不同的初速度va、vb、vc从A点沿图示方向射入该磁场区域,经磁场偏转后粒子a、b、c分别从BC边中点、CD边中点、AD边中点射出.若ta、tb、tc分别表示粒子a、b、c在磁场中的运动时间.则以下判断正确的是( )
A.va<vb<vc
B.vc<vb<va
C.ta<tb<tc
D.ta=tb<tc
答案
粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:qvB=m
,v=v2 R
,qBR m
粒子做圆周运动的周期:T=
,由于三个粒子完全相同,则它们做圆周运动的周期T相等,2πm qB
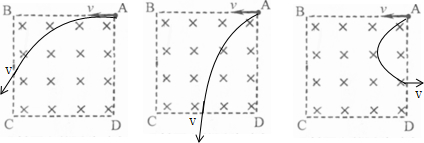
如图所示,粒子的轨道半径:R1<R2<R3,vc<vb<va,故A错误,B正确;
粒子在磁场中做圆周运动转过的圆心角间的关系为:θ1<θ2<θ3,
粒子运动时间t=
T,则粒子在磁场中的运动时间:t1<t2<t3,故C正确,D错误;θ 2π
故选:BC.
