问题
问答题
如图所示，在空间存在这样一个磁场区域，以MN为界，上部分的匀强磁场的磁感应强度为B1，下部分的匀强磁场的磁感应强度为B2，B1=2B2=2B0，方向均垂直纸面向内，且磁场区域足够大。在距离界线为h的P点有一带负电荷的离子处于静止状态，某时刻该离子分解成为带电荷的粒子A和不带电的粒子B，粒子A质量为m、带电荷q，以平行于界线MN的速度向右运动，经过界线MN时的速度方向与界线成60°角，进入下部分磁场。当粒子B沿与界线平行的直线到达位置Q点时，恰好又与粒子A相遇。不计粒子的重力。求：
（1）P、Q两点间距离。
（2）粒子B的质量。
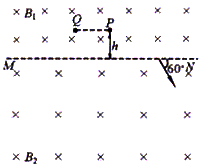
答案
（1）
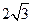h （2）
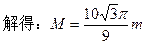
（1）粒子A在匀强磁场中做匀速圆周运动，洛仑兹力提供向心力，设粒子A的速度为v0，在MN上方运动半径为R1，运动周期为T1，根据牛顿第二定律和圆周运动公式：
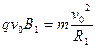
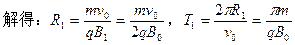（2分）
同理，粒子A在MN下方运动半径R2和周期T2分别为：
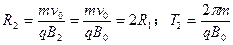
粒子A由P点运动到MN边界时与MN的夹角为60°，如答图2所示，则有：R1－h=R1cos60°。
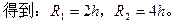
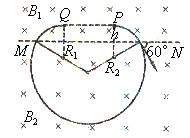
图2
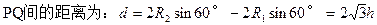（3分）
（2）粒子A从P点到Q点所用时间为：
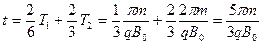（1分）
（1分）
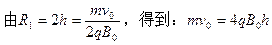
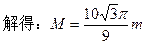（2分）