（1）f′（x）=（x-1）²+2x（x-1）=3x²-4x+1=（3x-1）（x-1），x＞0．令f′（x）=0，得x=

1

3

或x=1，f（x），f′（x）随x的变化情况如下表

∴当x=

1

3

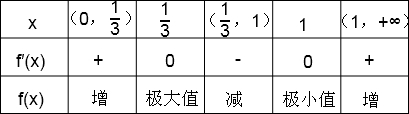
时，有极大值f（

1

3

）=

4

27

，当x=1时，有极小值f（1）=0．

（2）由（1）知：f（x）在（0，

1

3

]，[1，+∞）上是增函数，在[

1

3

，1]上是减函数，

①0＜a≤

1

3

时，F（a）=a（a-1）²，G（a）=（a-1）²≥

4

9

特别的，当a=

1

3

时，有G（a）=

4

9

，

②当

1

3

＜a≤1时，F（a）=f（

1

3

）=

4

27

，G（a）=

4 27

a

≥

4

27

特别的，当a=1时，有G（a）=

4

27

，

由①②知，当0＜a≤1时，函数G(a)=

F(a)

a

的最小值为

4

27

．

（3）由已知得h₁（x）=x+m-g（x）=2x²-3x-lnx+m-t≥0在（0，+∞）上恒成立，

∵h′1(x)=

(4x+1)(x-1)

x

，

∴x∈（0，1）时，h′₁（x）＜0，x∈（1，+∞）时，h₁（x）＞0

∴x=1时，h′₁（x）取极小值，也是最小值，

∴当h₁（1）=m-t-1≥0，m≥t+1时，h₁（x）≥0在（0，+∞）上恒成立，

同样，h₂（x）=f（x）-x-m=x³-2x²-m≥0在（0，+∞）上恒成立，

∵h′₂（x）=3x（x-

4

3

），

∴x∈（0，

4

3

）时，h′₂（x）＜0，x∈（

4

3

，+∞），h′₂（x）＞0，

∴x=

4

3

时，h₂（x）取极小值，也是最小值，

∴h2(

4

3

)=-

32

27

-m≥0，m≤-

32

27

时，h₂（x）≥0在（0，+∞）上恒成立，

∴t+1≤m≤-

32

27

，

∵实数m有且只有一个，∴m=-

32

27

，t=-

59

27

．