问题
问答题
如图所示，一质量为m，带电荷量为+q的粒子以速度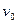
从O点沿y轴正方向射入磁感应强度为B的圆形匀强磁场区域，磁场方向垂直纸面向外，粒子飞出磁场区域后，从点b处穿过x轴，速度方向与x轴正方向的夹角为30°，同时进入场强为E、方向沿x轴负方向成60°角斜向下的匀强电场中，通过了b点正下方的c点，如图所示．粒子的重力不计，试求：
⑴圆形匀强磁场的最小面积．
⑵粒子在磁场中运动的时间.
⑶c点到b点的距离d．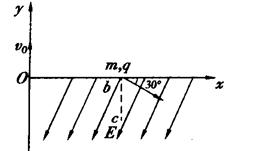
答案
（1）
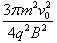（2）
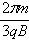（3）
⑴粒子在磁场中做匀速圆周运动，轨迹半径为R，则有R=
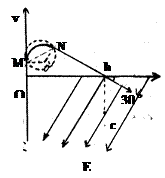
粒子经过磁场区域速度偏转角为120°，这表明在磁场区域中轨迹为半径为R的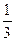
圆弧，此圆弧应与入射和出射方向相切．作出粒子运动轨迹如图中实线所示．轨迹MN为以O′为圆心、R为半径，且与两速度方向相切的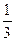圆弧，M、N两点还应在所求磁场区域的边界上．
在过M、N两点的不同圆周中，最小的一个是以MN为直径的圆周，所求圆形磁场区域的最小半径为
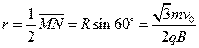2分
面积为S=
2分
⑵带电粒子在磁场中轨迹圆弧对应的圆心角为1200，带电粒子在磁场中运动的时间为转动周期的，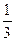
(2分)
⑶粒子进入电场做类平抛运动,设从b到c垂直电场方向位移x′，沿电场方向位移y′,所用时间为t,则有x′=v0t
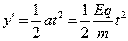2分
又
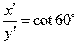2分
解得 x′=
mv02/Eq
y′=6mv02/Eq 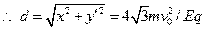2分
2分