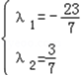问题
解答题
设a=（﹣1，1），b=（4，3），c=（5，﹣2），
（1）求证a与b不共线，并求a与b的夹角的余弦值；
（2）求c在a方向上的投影；
（3）求λ1和λ2，使c=λ1a+λ2b
答案
解：（1）∵a=（﹣1，1），b=（4，3），且﹣1×3≠1×4，
∴a与b不共线．又a·b=﹣1×4+1×3=﹣1，|a|=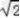
，|b|=5，
∴cos＜a，b＞=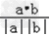
=
=﹣
．
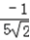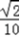（2）∵a·c=﹣1×5+1×（﹣2）=﹣7，
∴c在a方向上的投影为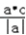 
=
=﹣
．
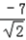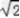（3）∵c=λ1a+λ2b，
∴（5，﹣2）=λ1（﹣1，1）+λ2（4，3） =（4λ2﹣λ1，λ1+3λ2），
∴
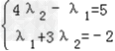，解得