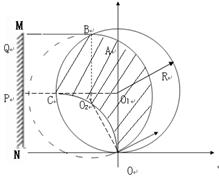
如图所示，质量为m=8.0×10-25kg，电荷量为q=1.6×10-15C的带正电粒子从坐标原点O处沿xOy平面射入第一象限内，且与x方向夹角大于等于300的范围内，粒子射入时的速度方向不同，但大小均为v0=2.0×107m/s.现在某一区域内加一方向向里且垂直于xOy平面的匀强磁场，磁感应强度大小为B=0.1T，若这些粒子穿过磁场后都能射到与y轴平行的荧光屏MN上，并且当把荧光屏MN向左移动时，屏上光斑长度和位置保持不变。求：
(1) 粒子从y轴穿过的范围；
(2) 荧光屏上光斑的长度；
(3) 从最高点和最低点打到荧光屏MN上的粒子运动的时间差。
(4)画出所加磁场的最小范围（用斜线表示）
(1) 0---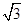
R (2)
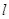=(1+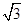) R (3) t=（
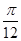+0. 5）×10-8S
(4)
设磁场中运动的半径为R，牛顿第二定律得：
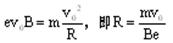
解得R=0.1m (2分)
当把荧光屏MN向左移动时，屏上光斑长度和位置保持不变,说明电子出射方向平行，都沿-x方向，所加磁场为圆形，半径为R=0.1。 (1分)
(1)电子从y轴穿过的范围 :
初速度沿y轴正方向的粒子直接过y轴 (1分)
速度方向在与x方向成300的粒子，转过的角OO2A 为1200， (2分)
粒子从y轴穿过的范围 0---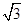R (1分)
(2)如图所示，初速度沿y轴正方向的粒子， yC=R (1分)
速度方向在与x方向成300的粒子，转过的圆心角OO2B为1500 O2OA=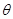
=300
yB=R+Rcosθ (2分)
荧光屏上光斑的长度 (1+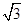) R (2分)
(3)例子旋转的周期 T=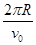
=
=
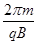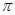×10-8S (1分)
在磁场中的时间差 t1=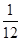
T (1分)
出磁场后，打到荧光屏的时间差 t2=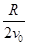
(1分)
从最高点和最低点打到荧光屏MN上的粒子运动的时间差。
t= t1- t2=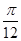（+0. 5）×10-8S (1分)
（4）范围见答案图